17. 基于时间的反向传播算法(第二部分)
我们现在展开模型。你会发现基于时间的展开模型非常有利于可视化基于时间的反向传播算法过程中所需的步长数(转换为乘法)。这些乘法运算来自链式法则 ,而且使用这个模型很容易实现可视化。
在这个视频中,我们将了解调整两个权重矩阵时,如何使用基于时间的反向传播算法:
- W_y - 连接状态和输出的权重矩阵
- W_s - 连接一个状态和下一个状态的权重矩阵
20 循环神经网络:基于时间的反向传播算法 B V5 最后一节
展开模型非常有利于可视化基于时间的反向传播算法。

时间步长 3 的展开模型
调整W_y所需的梯度计算
通过简单的一步链式法则,可以得到对于W_y 损失函数的偏导数:
(请注意,在这个例子中,我们不需要使用基于时间的反向传播算法。计算路径的可视化可在本视频中找到)。
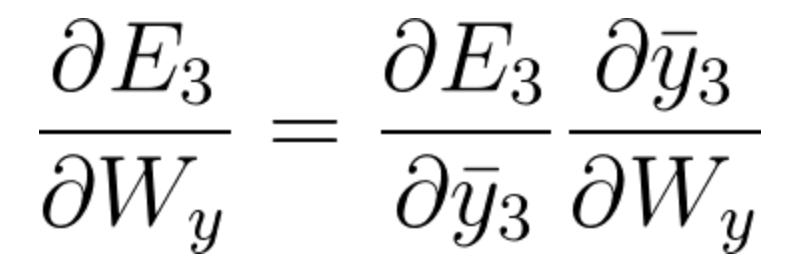
方程式 36
一般来说,我们可以追溯多个时间步长,而不是像这个例子那样只有3个时间步长。对于任意时间步长N,调整W_y所需的梯度计算为:
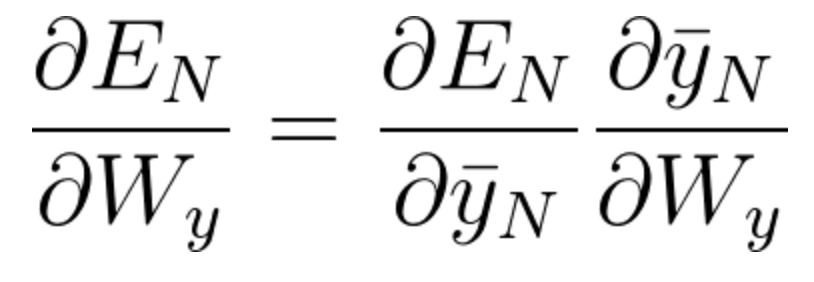
方程式 37
调整W_s所需的梯度计算
我们仍然需要调整连接一个状态和下一个状态的权重矩阵W_s以及连接输入和状态的权重矩阵W_x。我们可以任意从W_s开始。
为了理解基于时间的反向传播算法过程,我们可以简化展开模型。我们将重点介绍W_s对输出的贡献,具体如下:
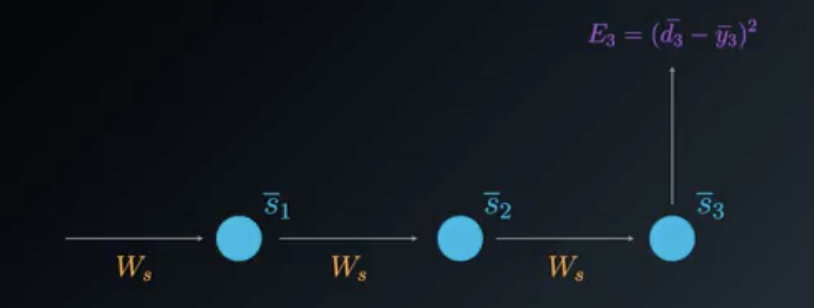
调整 Ws 的简化展开模型
计算W_s损失函数的偏导数时,我们需要考虑有利于输出的所有状态。这个例子中,状态\bar{s_3}取决于之前的状态\bar{s_2},而之前的状态也取决于前面的\bar{s_1},即第一个状态。
基于时间的反向传播算法中,我们将考虑每个状态的每个梯度,累加所有这些贡献。
- 在时间步长t = 3时,对来自\bar{s_3}的梯度贡献如下:
(请注意这里使用链式法则。如果需要,请返回视频以查看计算路径)。
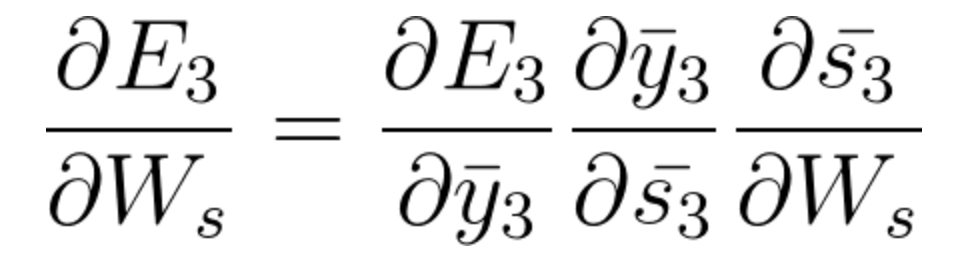
方程式38
- 时间步长 t=3 时,对来自\bar{s_2}的梯度贡献如下:
(请注意,链式法则推导的方程式如何考虑\bar{s_2}对\bar{s_3}的贡献。如果需要,请返回视频以查看计算路径)。
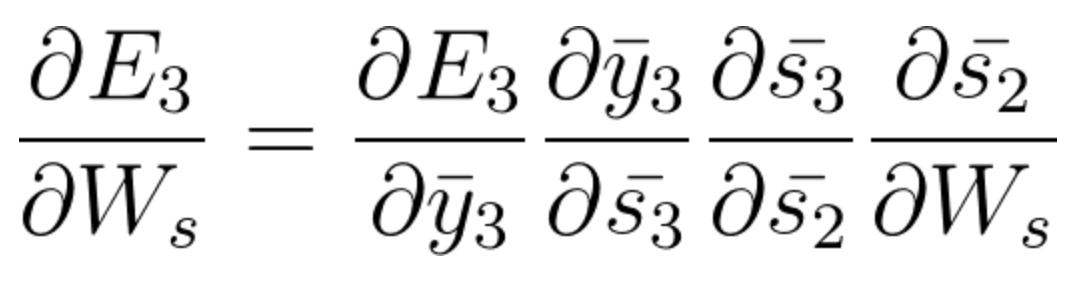
方程式39
- 时间步长 t=3 时,来自\bar{s_1}的梯度贡献如下:
(链式法则推导的方程式如何考虑\bar{s_1}和\bar{s_2} and \bar{s_3}的贡献。如果需要,请返回视频以查看计算路径)。
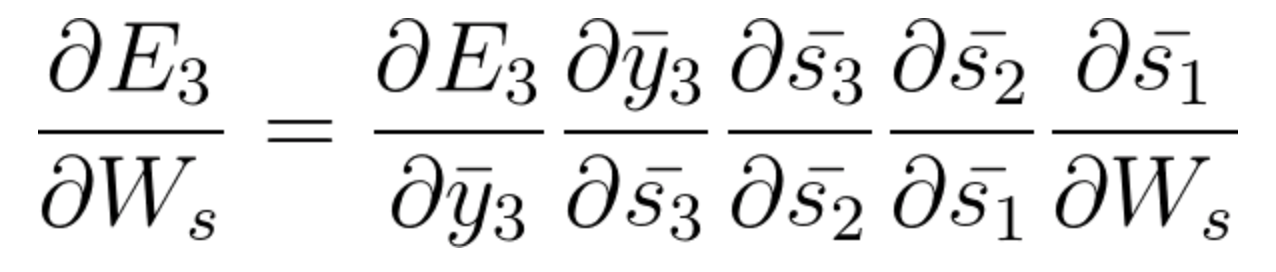
方程式40
考虑以下三个状态的贡献后:\bar{s_3}、\bar{s_2}和\bar{s_1},我们将累加它们来找到最终的梯度计算。
下列方程式是使用基于时间的反向传播算法来调整W_s的梯度:
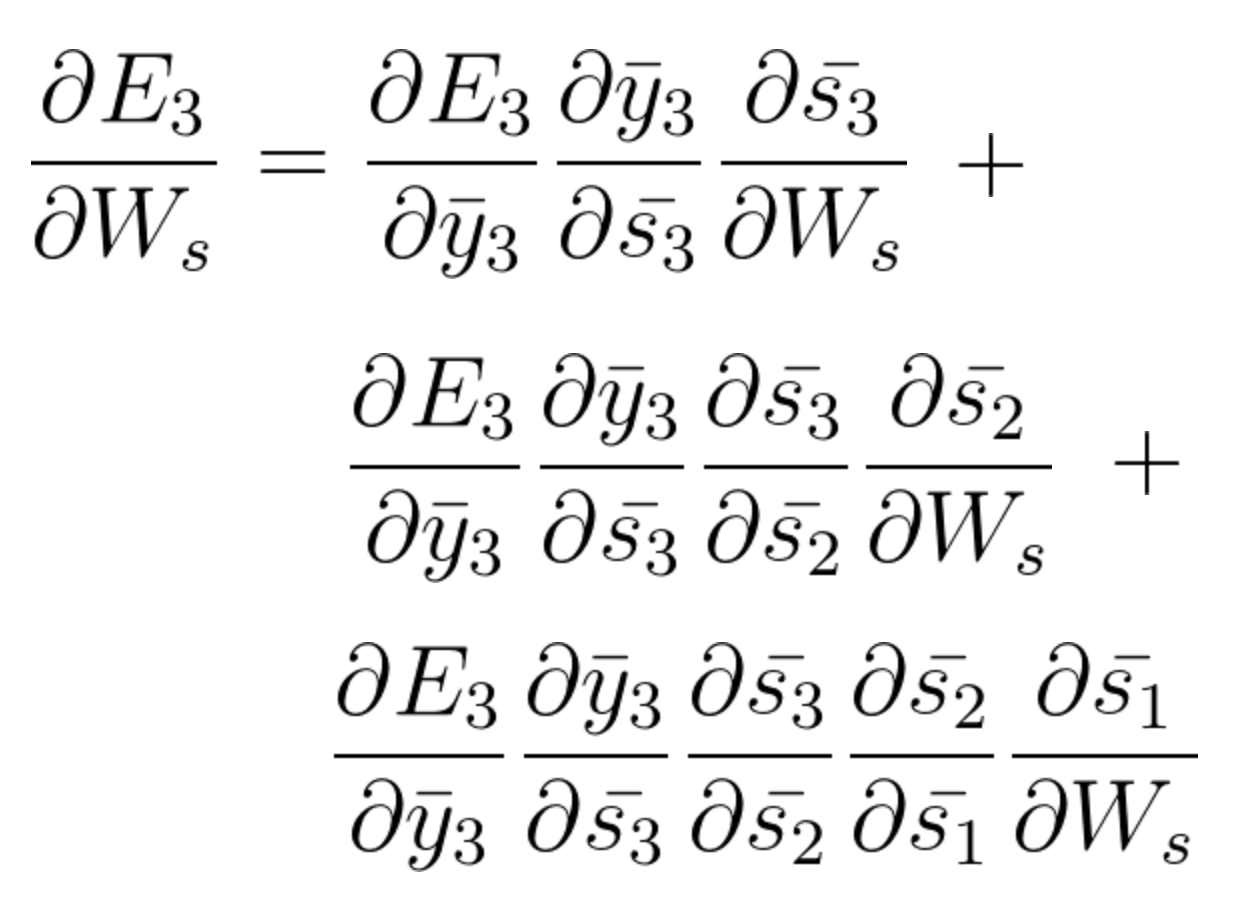
方程式 41
这个例子中,我们需要考虑三个时间步长,所以我们累加了三个偏导数的计算。一般来说,我们可以追溯多个时间步长。如果仔细观察方程式38、39和40,你会发现一种模式。你会发现,当反向退后一步,我们在链式法则中就需要考虑一个额外的偏导数。从数学角度上来说,这可以用下面的通用方程式表示,使用**基于时间的反向传播算法 **来调整W_s:
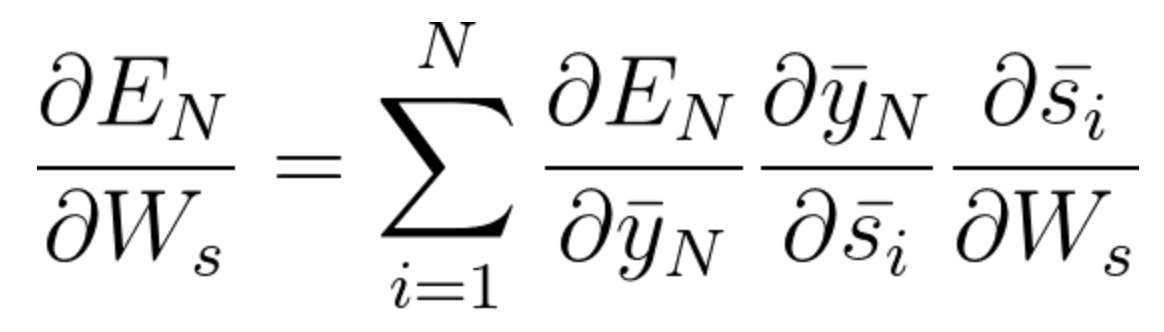
方程式42
请注意,方程式42 考虑了后退 N 步的一般集合。正如这个课程所提到的,由于梯度消失的问题,采集超过8到10步长的关系实际上是不可能的。我们将在马上开始的长短期记忆网络部分,讨论解决这个问题的方法。
我们仍然需要调整连接输入和状态的权重矩阵 W_x。
休息一下。你可以利用这段时间来温习下目前我们已经学习的基于时间的反向传播算法过程。试着掌握这些数学知识。
一旦掌握了刚刚观看的视频内容,请独立尝试推导调整最后一个矩阵W_x的计算。这不是强制性要求,但是如果你觉得自己能应对挑战,那就来吧!对比你和我们的注释,会非常有趣。
如果你选择接受挑战,请专注于简化展开模型,只保留计算所需的内容。绘制反向传播"路径"概略图,一步步思考链式法则如何解决这些导数。不要忘记累加!